proximately what is the area under the curve to the right of the vertical line

In probability theory and statistics, the Normal Distribution, also chosen the Gaussian Distribution, is the most pregnant continuous probability distribution. Sometimes it is also called a bell curve. A big number of random variables are either nigh or exactly represented past the normal distribution, in every physical science and economics. Furthermore, it tin can exist used to estimate other probability distributions, therefore supporting the usage of the word 'normal 'as in about the one, mostly used.

Table of Contents:

• Definition
• Formula
• Curve
• Normal Distribution Standard Deviation
• Table
• Problems and Solutions
• Backdrop
• Applications
• FAQs

Normal Distribution Definition

The Normal Distribution is defined by the probability density part for a continuous random variable in a system. Permit united states of america say, f(ten) is the probability density function and X is the random variable. Hence, it defines a function which is integrated between the range or interval (x to ten + dx), giving the probability of random variable X, by considering the values between ten and x+dx.

f(x) ≥ 0 ∀ x ϵ (−∞,+∞)

And _-∞∫^+∞ f(x) = i

Normal Distribution Formula

The probability density role of normal or gaussian distribution is given by;

Where,

• x is the variable
• μ is the mean
• σ is the standard deviation

As well, read:

• Standard Normal Distribution
• Uniform Distribution
• Beta Distribution
• Cumulative Frequency Distribution
• Exponential Distribution
• Frequency Distribution Table
• Probability For Class 12

Normal Distribution Curve

The random variables following the normal distribution are those whose values can notice any unknown value in a given range. For example, finding the tiptop of the students in the school. Here, the distribution can consider any value, but it will exist divisional in the range say, 0 to 6ft. This limitation is forced physically in our query.

Whereas, the normal distribution doesn't even bother virtually the range. The range tin likewise extend to –∞ to + ∞ and still we tin find a smooth bend. These random variables are called Continuous Variables, and the Normal Distribution then provides here probability of the value lying in a particular range for a given experiment. Likewise, apply the normal distribution calculator to observe the probability density function by just providing the mean and standard divergence value.

Normal Distribution Standard Deviation

Mostly, the normal distribution has any positive standard deviation. We know that the mean helps to decide the line of symmetry of a graph, whereas the standard deviation helps to know how far the data are spread out. If the standard deviation is smaller, the data are somewhat close to each other and the graph becomes narrower. If the standard deviation is larger, the data are dispersed more than, and the graph becomes wider. The standard deviations are used to subdivide the area nether the normal curve. Each subdivided department defines the percentage of data, which falls into the specific region of a graph.

Using 1 standard divergence, the Empirical Rule states that,

• Approximately 68% of the information falls within one standard deviation of the mean. (i.e., Between Mean- one Standard Deviation and Hateful + one standard departure)
• Approximately 95% of the information falls within two standard deviations of the mean. (i.east., Between Mean- ii Standard Deviation and Mean + two standard deviations)
• Approximately 99.7% of the information fall within three standard deviations of the mean. (i.due east., Between Hateful- iii Standard Deviation and Mean + iii standard deviations)

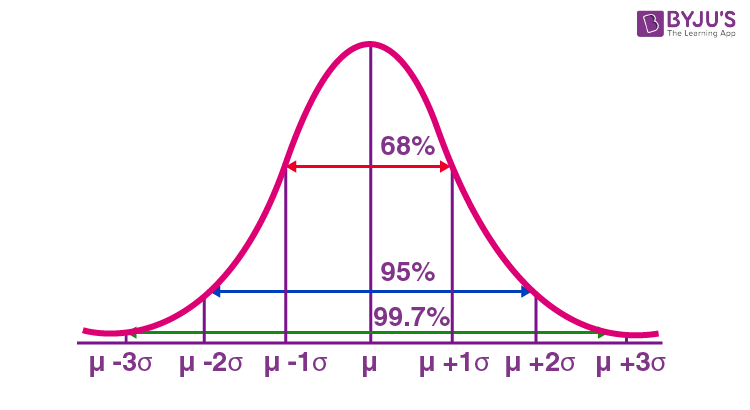
Thus, the empirical rule is also called the 68 – 95 – 99.7 rule.

Normal Distribution Table

The tabular array here shows the expanse from 0 to Z-value.

Z-Value	0.00	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0.0000	0.0040	0.0080	0.0120	0.0160	0.0199	0.0239	0.0279	0.0319	0.0359
0.1	0.0398	0.0438	0.0478	0.0517	0.0557	0.0596	0.0636	0.0675	0.0714	0.0753
0.2	0.0793	0.0832	0.0871	0.0910	0.0948	0.0987	0.1026	0.1064	0.1103	0.1141
0.3	0.1179	0.1217	0.1255	0.1293	0.1331	0.1368	0.1406	0.1443	0.1480	0.1517
0.4	0.1554	0.1591	0.1628	0.1664	0.1700	0.1736	0.1772	0.1808	0.1844	0.1879
0.5	0.1915	0.1950	0.1985	0.2019	0.2054	0.2088	0.2123	0.2157	0.2190	0.2224
0.half-dozen	0.2257	0.2291	0.2324	0.2357	0.2389	0.2422	0.2454	0.2486	0.2517	0.2549
0.7	0.2580	0.2611	0.2642	0.2673	0.2704	0.2734	0.2764	0.2794	0.2823	0.2852
0.8	0.2881	0.2910	0.2939	0.2967	0.2995	0.3023	0.3051	0.3078	0.3106	0.3133
0.9	0.3159	0.3186	0.3212	0.3238	0.3264	0.3289	0.3315	0.3340	0.3365	0.3389
1.0	0.3413	0.3438	0.3461	0.3485	0.3508	0.3531	0.3554	0.3577	0.3599	0.3621
1.1	0.3643	0.3665	0.3686	0.3708	0.3729	0.3749	0.3770	0.3790	0.3810	0.3830
one.2	0.3849	0.3869	0.3888	0.3907	0.3925	0.3944	0.3962	0.3980	0.3997	0.4015
1.3	0.4032	0.4049	0.4066	0.4082	0.4099	0.4115	0.4131	0.4147	0.4162	0.4177
1.four	0.4192	0.4207	0.4222	0.4236	0.4251	0.4265	0.4279	0.4292	0.4306	0.4319
one.5	0.4332	0.4345	0.4357	0.4370	0.4382	0.4394	0.4406	0.4418	0.4429	0.4441
1.half dozen	0.4452	0.4463	0.4474	0.4484	0.4495	0.4505	0.4515	0.4525	0.4535	0.4545
one.seven	0.4554	0.4564	0.4573	0.4582	0.4591	0.4599	0.4608	0.4616	0.4625	0.4633
1.viii	0.4641	0.4649	0.4656	0.4664	0.4671	0.4678	0.4686	0.4693	0.4699	0.4706
1.9	0.4713	0.4719	0.4726	0.4732	0.4738	0.4744	0.4750	0.4756	0.4761	0.4767
ii.0	0.4772	0.4778	0.4783	0.4788	0.4793	0.4798	0.4803	0.4808	0.4812	0.4817
two.one	0.4821	0.4826	0.4830	0.4834	0.4838	0.4842	0.4846	0.4850	0.4854	0.4857
ii.2	0.4861	0.4864	0.4868	0.4871	0.4875	0.4878	0.4881	0.4884	0.4887	0.4890
2.3	0.4893	0.4896	0.4898	0.4901	0.4904	0.4906	0.4909	0.4911	0.4913	0.4916
2.iv	0.4918	0.4920	0.4922	0.4925	0.4927	0.4929	0.4931	0.4932	0.4934	0.4936
2.five	0.4938	0.4940	0.4941	0.4943	0.4945	0.4946	0.4948	0.4949	0.4951	0.4952
2.6	0.4953	0.4955	0.4956	0.4957	0.4959	0.4960	0.4961	0.4962	0.4963	0.4964
2.seven	0.4965	0.4966	0.4967	0.4968	0.4969	0.4970	0.4971	0.4972	0.4973	0.4974
2.eight	0.4974	0.4975	0.4976	0.4977	0.4977	0.4978	0.4979	0.4979	0.4980	0.4981
two.nine	0.4981	0.4982	0.4982	0.4983	0.4984	0.4984	0.4985	0.4985	0.4986	0.4986
3.0	0.4987	0.4987	0.4987	0.4988	0.4988	0.4989	0.4989	0.4989	0.4990	0.4990

Normal Distribution Problems and Solutions

Question 1: Summate the probability density function of normal distribution using the post-obit data. ten = iii, μ = 4 and σ = 2.

Solution: Given, variable, x = 3

Mean = 4 and

Standard difference = 2

By the formula of the probability density of normal distribution, we can write;

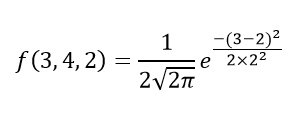
Hence, f(three,4,2) = ane.106.

Question 2: If the value of random variable is 2, hateful is 5 and the standard deviation is 4, then observe the probability density office of the gaussian distribution.

Solution: Given,

Variable, x = ii

Mean = v and

Standard deviation = four

By the formula of the probability density of normal distribution, we can write;

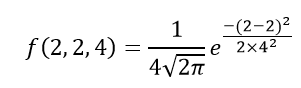
f(two,two,four) = ane/(four√2π) due east⁰

f(2,2,iv) = 0.0997

There are two main parameters of normal distribution in statistics namely mean and standard divergence. The location and scale parameters of the given normal distribution can exist estimated using these ii parameters.

Normal Distribution Backdrop

Some of the of import properties of the normal distribution are listed below:

• In a normal distribution, the mean, mean and style are equal.(i.e., Mean = Median= Mode).
• The total area under the curve should exist equal to 1.
• The normally distributed bend should exist symmetric at the centre.
• There should be exactly half of the values are to the correct of the heart and exactly one-half of the values are to the left of the centre.
• The normal distribution should be defined by the mean and standard deviation.
• The normal distribution curve must have only one top. (i.e., Unimodal)
• The bend approaches the 10-axis, but it never touches, and information technology extends farther away from the mean.

Applications

The normal distributions are closely associated with many things such as:

• Marks scored on the test
• Heights of different persons
• Size of objects produced past the machine
• Blood pressure then on.

Often Asked Questions on Normal Distribution – FAQs

What is a normal distribution in statistics?

A probability function that specifies how the values of a variable are distributed is chosen the normal distribution. It is symmetric since well-nigh of the observations assemble around the key peak of the curve. The probabilities for values of the distribution are afar from the mean narrow off evenly in both directions.

What does normal distribution hateful?

In statistics (and in probability theory), the Normal Distribution, also called the Gaussian Distribution, is the most important continuous probability distribution. Sometimes it is as well called a bell curve.

What is a normal distribution used for?

A normal distribution is meaning in statistics and is oft used in the natural sciences and social arts to draw real-valued random variables whose distributions are unknown.

What are the characteristics of a normal distribution?

The essential characteristics of a normal distribution are:
Information technology is symmetric, unimodal (i.eastward., 1 mode), and asymptotic.
The values of mean, median, and mode are all equal.
A normal distribution is quite symmetrical nigh its center. That means the left side of the center of the superlative is a mirror image of the right side. There is too only ane peak (i.east., one way) in a normal distribution.

How do you lot know if information is normally distributed?

A histogram presents a useful graphical representation of the given information. When a histogram of distribution is superimposed with its normal curve, so the distribution is known equally the normal distribution.

How practice yous use a normal distribution table?

As we know, the label for rows contains the integer role and the first decimal place of z. In dissimilarity, the title for columns comprises the second decimal place of z. The values within the tabular array are the probabilities respective to the tabular array type. Hence, to get the value of 0.56 from the z-table, place the probability value corresponding to the 0.v row and 0.06 column (=0.2123).

holidayoffinto.blogspot.com

Source: https://byjus.com/maths/normal-distribution/

Share this post